如何在不规则多边形内均匀撒点的算法
给定一个不规则的多边形（可能是凹多边形，可能是凸多边形），在其中要显示拓扑网络数据，要求节点不重合、不超出边界。
该问题出现的场景：
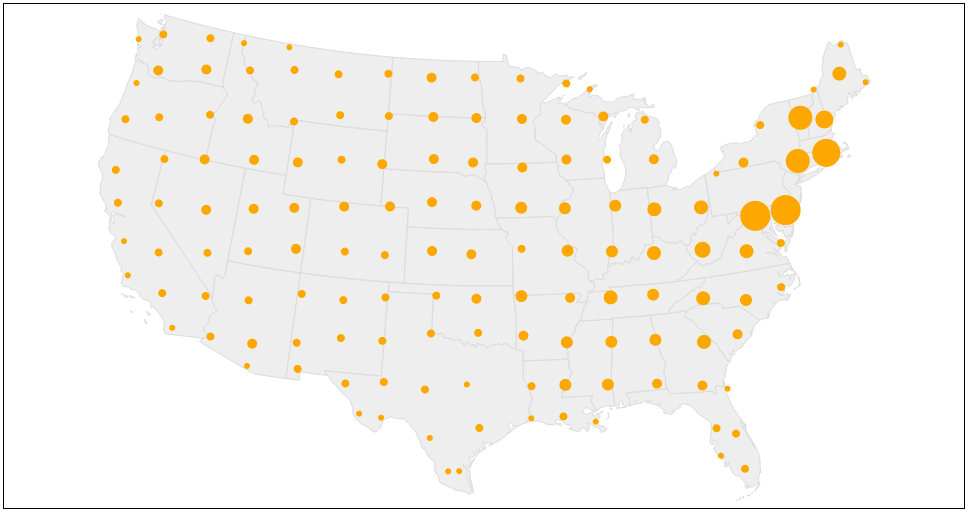
- 在地图上撒点
- 在未知画布上生成初始的拓扑布局
解决方案：
方法一 随机撒点
取凸多边形的外接矩形，在矩形中随机撒点，如果落在凸多边形外，再次随机撒点，直至落在凸多边形内。 这个方法比较暴力，可以通过计算期望来控制撒点次数，撒点次数应该符合泊松分布。
方法二 把不规则多边形切割成若干三角形
可以看作方法一的改进。切成多个三角形之后，问题转化为了如何在多个三角形内撒点。
参考：https://beta.observablehq.com/@scarysize/finding-random-points-in-a-polygon (opens in a new tab) 切割库：https://github.com/mapbox/earcut (opens in a new tab)
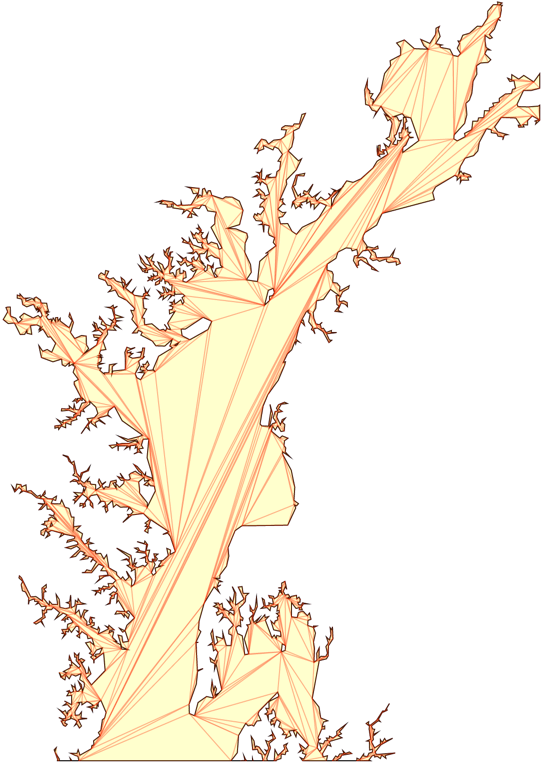
三角形是凸多边形，如何在三角形内均匀撒点可参考：http://mathworld.wolfram.com/TrianglePointPicking.html (opens in a new tab)
算法步骤：
- 随机选取任意一三角形
- 在三角形内撒点
- 重复 12，直到点撒完
这里有个问题*：每个三角形被选取的概率相同，但三角形面积不同。这就可能出现小面积三角形中的点和大面积三角形中的点个数差不多，从而造成总体上看起来点集中在小面积三角形中的情况。 所以要保证三角形被选取的概率跟它的面积成正比。
方法三 用力导向迭代
可以看作是 方法二 的改进。给随机撒好的点设置相同的电荷力，使其不停迭代到稳定状态，即形成下图状态，达到尽量“均匀”。
参考：https://bl.ocks.org/mbostock/1b64ec067fcfc51e7471d944f51f1611 (opens in a new tab)
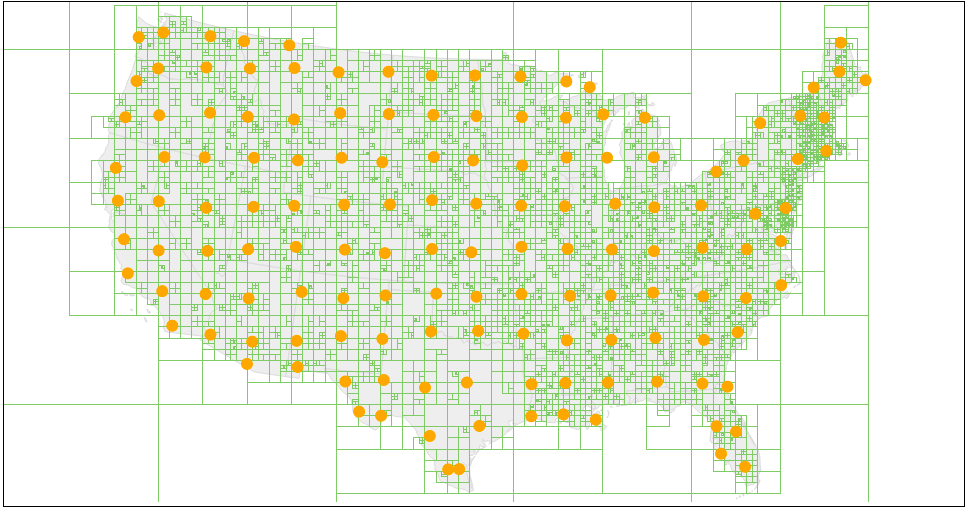
方法四 用四叉树生成点
和前三种方法无关。用四叉树将二维空间切割成相等大小的正方形，然后用正方形图心撒点。
